A Beginner's Guide To Using ngrx In An Ionic 2+ App - Part 1
In this tutorial, we'll have a look at what ngrx is and how it can help you manage application state in your Ionic 2 app, or any other Angular 2 app for that matter.
This tutorial is part of a multi-part series:
Part 1 - Setting up Store, Actions and Reducers (this post)
Part 2 - Persisting to a PouchDB database
==Update: The code in this tutorial is now up to date with Ionic 2.0.0-rc.4 (December 2016)==
In my previous post I made a birthday tracker app that lets you add, update and delete birthdays, which were persisted with the PouchDB library. We'll be creating the exact same application, but this time, we'll use ngrx to manage the application state.
Why ngrx?
ngrx is based on Redux, a very popular library (and design pattern) that was created to manage application state in React applications.
The redux design pattern defines the use of an in-memory object, called a store, that keeps track of the state of the application. You can think of it as an in-memory database for your app.
To manage the state of the application there are actions and reducers. Whenever state needs to change, an action is invoked, this action will be dispatched to the store, which then uses a reducer function to update the state. The store then allows other components to subscribe to it to receive these updates.
Let's have a look at an example in the context of the app that we are going to build.
We have an array of Birthday objects on the store which represents the current state. When the user adds a new Birthday, we dispatch the action ADD_BIRTHDAY along with the new Birthday object to the store, which then uses the BirthdayReducer function to change the state to include the new Birthday object.
The important thing to note here is that actions go up to the store and data flows down from the store.
The ngrx libary uses RxJS to implement this design pattern for Angular 2 applications. The library is split up is several building blocks, the one that is relevant for this part of the tutorial is @ngrx/store.
I've placed links to good resources on learning more about ngrx at the end of this post.
Using ngrx in your app will make it easier to debug issues because the only place where state can change is in the reducer. The reducer functions are also very easy to test in isolation because given the same input they will always return the same output (they are pure functions).
Components subscribe to the store through an Observable to receive state changes. Having a unidirectional data flow means that you can configure the Angular 2 change detector for these components to OnPush, which can radically improve the performance of your app.
For a better understanding of change detection read this.
If you find it hard to wrap your head around all of this, don't worry, it will hopefully make more sense when we go through the code, so let's get started!
###Let's build our app We'll start by creating our Ionic 2 app.
$ ionic start ionic2-tutorial-ngrx blank --v2
$ cd ionic2-tutorial-ngrxIonic 2 apps are now created as TypeScript apps by default, no need to include the
--tsanymore!
Install @ngrx/store
Next, we need to install the @ngrx/store library. This will also install the @ngrx/core dependency.
$ npm install @ngrx/core @ngrx/store --saveDefine Birthday
Before we build anything, let's first define what a Birthday object is, so we can use it in our actions and reducer.
// location: src/models/birthday.ts
export interface Birthday {
Name: string;
Date: Date;
}Define AppState
Next, we'll define the application state which will be managed by the store.
In our case this will only contain an array of Birthday objects, but it can contain anything you define as state for your application. For instance, keeping track of the selected Birthday could also be managed by the store.
// location: src/services/app-state.ts
import {Birthday} from '../models/birthday';
export interface AppState {
birthdays: Birthday[];
}Define Actions
An action is anything that can happen that has an effect on the application state. In this part of the tutorial, we can have the following actions:
- Add a birthday
- Update a birthday
- Delete a birthday
These actions will be dispatched to the store which will then call the reducer to update the birthdays array with the action.
An action has a type, which is just a string that identifies the action and a payload, which, in this case, will be a Birthday object.
// location: src/actions/birthday.actions.ts
import {Injectable} from '@angular/core';
import {Action} from '@ngrx/store';
import {Birthday} from '../models/birthday';
@Injectable()
export class BirthdayActions {
static ADD_BIRTHDAY = 'ADD_BIRTHDAY';
addBirthday(birthday: Birthday): Action {
return {
type: BirthdayActions.ADD_BIRTHDAY,
payload: birthday
}
}
static UPDATE_BIRTHDAY = 'UPDATE_BIRTHDAY';
updateBirthday(birthday: Birthday): Action {
return {
type: BirthdayActions.UPDATE_BIRTHDAY,
payload: birthday
}
}
static DELETE_BIRTHDAY = 'DELETE_BIRTHDAY';
deleteBirthday(birthday: Birthday): Action {
return {
type: BirthdayActions.DELETE_BIRTHDAY,
payload: birthday
}
}
}Create the Reducer
A reducer function takes the current state of the data it's responsible for, makes a modification depending on the action and returns the new state.
So in our case, this specific reducer is responsible for keeping the birthdays state up-to-date.
In the code below you can see that initially, the state will be an empty array. Depending on the action, we then create a new array that will contain the updated state. The store will keep track of this state, which is the birthdays array as defined in AppState, and pass it into the reducer when an action is received.
// location: app/reducers/birthdays.reducer.ts
import {ActionReducer, Action} from '@ngrx/store';
import {BirthdayActions} from '../actions/birthday.actions';
let nextId = 0;
export function BirthdaysReducer(state = [], action) {
switch(action.type) {
case BirthdayActions.ADD_BIRTHDAY:
return [...state, Object.assign({}, action.payload, { id: nextId++ })];
case BirthdayActions.UPDATE_BIRTHDAY:
return state.map(birthday => {
return birthday.id === action.payload.id ? Object.assign({}, birthday, action.payload) : birthday;
});
case BirthdayActions.DELETE_BIRTHDAY:
return state.filter(birthday => birthday.id !== action.payload.id);
default:
return state;
};
}It's important to remember that a reducer does not modify the current state, but always returns a new array with the updated state.
###Let's build the UI OK, so we have the store, actions and reducers set up which are responsible for managing the state, let's have a look at the UI.
We'll create 2 pages for our app, one to display the list of birthdays (HomePage) and one to add or edit a birthday (DetailsPage).
####HomePage
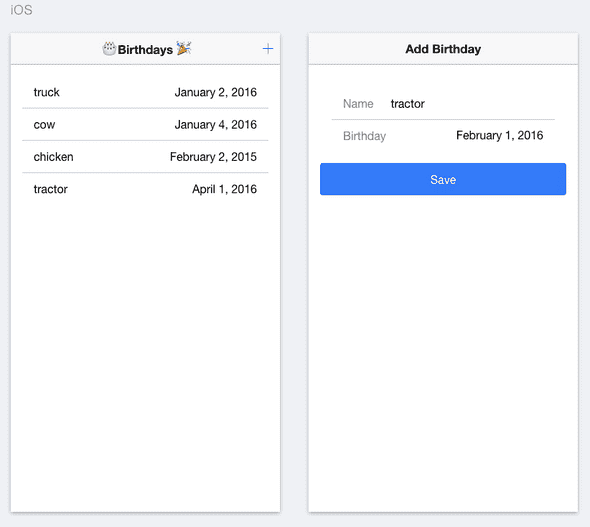
We'll implement the template home.html first, which uses an <ion-list> to display all the birthdays. Note that we are using the async pipe here, because birthdays will be an Observable.
<!-- location: src/pages/home/home.html -->
<ion-header>
<ion-navbar>
<ion-title>
🎂 Birthdays 🎉
</ion-title>
<ion-buttons end>
<button ion-button (click)="showDetail()">
<ion-icon name="add"></ion-icon>
</button>
</ion-buttons>
</ion-navbar>
</ion-header>
<ion-content class="home">
<ion-list inset>
<ion-item *ngFor="let birthday of birthdays | async" (click)="showDetail(birthday)">
<div item-left>{{ birthday.Name }}</div>
<div item-right>{{ birthday.Date | date:'yMMMMd' }}</div>
</ion-item>
</ion-list>
</ion-content>== Update: The following is not necessary anymore, because Safari 10 supports the Internationalization API.==
Angular 2 uses the Internationalization API to do date formatting, which is pretty cool, but doesn't work in Safari. So you have 2 options, you can either use this polyfill or write your own date formatting pipes. For this tutorial, we'll use the polyfill, which means that you need to add this line to your index.html.
<!-- location: src/index.html -->
<script src="https://cdn.polyfill.io/v2/polyfill.min.js?features=Intl.~locale.en"></script>Now it's time to open up home.ts and write the code to get the data from the store.
We are injecting the store here and all we need to do is select the birthdays state. And as mentioned before, we can now set the change detection strategy to OnPush.
// location: src/pages/home/home.ts
import { Component, ChangeDetectionStrategy } from "@angular/core";
import { ModalController, NavController } from 'ionic-angular';
import { Store } from '@ngrx/store';
import { Observable } from 'rxjs/rx';
import { AppState } from '../../services/app-state';
import { Birthday } from '../../models/birthday';
import { DetailsPage } from '../details/details';
@Component({
selector: 'page-home',
templateUrl: 'home.html',
changeDetection: ChangeDetectionStrategy.OnPush
})
export class HomePage {
public birthdays: Observable<Birthday[]>;
constructor(
private nav: NavController,
private store: Store<AppState>,
private modalCtrl: ModalController) {
this.birthdays = this.store.select(state => state.birthdays);
}
showDetail(birthday) {
let modal = this.modalCtrl.create(DetailsPage, { birthday: birthday });
modal.present();
}
}####DetailsPage Add a new page with this command:
$ ionic g page detailsAdd the following code in details.html, all it does is display the Name and the Date of the birthday.
<!-- location: src/pages/details/details.html -->
<ion-header>
<ion-navbar>
<ion-title>{{ action }} Birthday</ion-title>
<ion-buttons end *ngIf="!isNew">
<button ion-button (click)="delete()">
<ion-icon name="trash"></ion-icon>
</button>
</ion-buttons>
</ion-navbar>
</ion-header>
<ion-content padding class="details">
<ion-list>
<ion-item>
<ion-label>Name</ion-label>
<ion-input text-right type="text" [(ngModel)]="birthday.Name"></ion-input>
</ion-item>
<ion-item>
<ion-label>Birthday</ion-label>
<ion-datetime displayFormat="MMMM D, YYYY" pickerFormat="MMMM D YYYY" [(ngModel)]="isoDate"></ion-datetime>
</ion-item>
</ion-list>
<button ion-button block (click)="save()">Save</button>
</ion-content>Add the following code in details.ts.
As you can see, all we do here is let the store know when an action happened. The store will then call the reducer which will, in turn, return the new state to the store.
// location: src/pages/details/details.ts
import { Component } from '@angular/core';
import { NavParams, ViewController } from 'ionic-angular';
import { Store } from '@ngrx/store';
import { AppState } from '../../services/app-state';
import { BirthdayActions } from '../../actions/birthday.actions';
@Component({
selector: 'page-details',
templateUrl: 'details.html'
})
export class DetailsPage {
public birthday: any = {};
public isNew = true;
public action = 'Add';
public isoDate = '';
constructor(
private viewCtrl: ViewController,
private navParams: NavParams,
private store: Store<AppState>,
private birthdayActions: BirthdayActions) {
}
ionViewWillEnter() {
let editBirthday = this.navParams.get('birthday');
if (editBirthday) {
this.birthday = editBirthday;
this.isNew = false;
this.action = 'Edit';
this.isoDate = this.birthday.Date.toISOString().slice(0, 10);
}
}
save() {
this.birthday.Date = new Date(this.isoDate);
if (this.isNew) {
this.store.dispatch(this.birthdayActions.addBirthday(this.birthday));
}
else {
this.store.dispatch(this.birthdayActions.updateBirthday(this.birthday));
}
this.dismiss();
}
delete() {
this.store.dispatch(this.birthdayActions.deleteBirthday(this.birthday));
this.dismiss();
}
dismiss() {
this.viewCtrl.dismiss(this.birthday);
}
}Configure all dependencies
Modify app.module.ts.
// location: src/app/app.module.ts
import { NgModule, ErrorHandler } from '@angular/core';
import { IonicApp, IonicModule, IonicErrorHandler } from 'ionic-angular';
import { MyApp } from './app.component';
import { HomePage } from '../pages/home/home';
import { DetailsPage } from '../pages/details/details';
import { StoreModule } from '@ngrx/store';
import { BirthdaysReducer } from '../reducers/birthdays.reducer';
import { BirthdayActions } from '../actions/birthday.actions';
@NgModule({
declarations: [
MyApp,
HomePage,
DetailsPage
],
imports: [
IonicModule.forRoot(MyApp),
StoreModule.provideStore({ birthdays: BirthdaysReducer })
],
bootstrap: [IonicApp],
entryComponents: [
MyApp,
HomePage,
DetailsPage
],
providers: [{provide: ErrorHandler, useClass: IonicErrorHandler}, BirthdayActions]
})
export class AppModule {}###We're Done! You can now test the app in the browser.
$ ionic serveAnd on your iOS and Android devices.
$ ionic run ios
$ ionic run androidWhat's Next?
Now we have an app that can perform add/update/delete operations on our data, but the next time we start the app, all the data is gone. That kind of defeats the purpose of having a birthday tracker, so in the next part we'll have a look at using @ngrx/effects and PouchDB to persist the data.
####References
Reactive Angular 2 with ngRx: YouTube Video
@ngrx/store in 10 minutes: Egghead.io Free Video
Comprehensive Introduction to @ngrx/store
Example app showcasing the ngrx platform
Build a Better Angular 2 Application with Redux and ngrx
Everything is a stream: YouTube Video